（一）模糊理论

模糊理论主要内容包括模糊集合理论、模糊逻辑、模糊推理和模糊控制等。模糊理论是建立在模糊集合基础之上的，是描述和处理人类语言中所特有的模糊信息理论，其基本思想是把经典集合中的隶属关系加以扩充，把元素对“集合”的隶属程度由只能取0和1这两个值，推广到可以取区间[0，1]中的任意数值，从而实现定量地刻画模糊性对象。

在现实问题中，往往存在许多模糊的因素，与度量指标有关的目标数据很难获得，即便获得也要付出相当大的代价，况且获得的指标很难兼顾平衡性，而模糊集合理论则可以处理模棱两可或没有得到很好定义的数据，模糊方法可以不使用明确的数字而表达被选择准则或标准的相对重要性。利用近似信息或者不确定数据来做出决策，此时通常用的不确定数有区间数、三角模糊数、梯形模糊数，来构建模糊的应急决策方法。

在实际的决策过程中，人们往往根据目标的重要程度，对其属性的权重进行赋值，通常采用“不重要”“稍重要”“较重要”“重要”和“非常重要”五种语言性的衡量术语来估算每个指标的权重。在随后的模糊处理中，用模糊数来表示这些语言性的衡量术语。这些模糊数的定义分别为(0.0，0.1，0.3)，(0.1，0.3，0.5)，(0.3，0.5，0.7)，(0.5，0.7，0.9)和 (0.7，0.9，1.0)。

（二）灰色系统理论

灰色系统理论是研究部分信息已知、部分信息未知的系统，通过灰色关联分析、灰色预测等方法，寻找系统中蕴含的内在规律，以确定其系统中未知的部分，进而实现对数据的管理和控制。灰色系统理论认为，尽管客观系统表象极为复杂，表征数据看似杂乱无章，但是在系统内部必然存在着联系，蕴含着内在规律。灰色系统理论把社会系统、经济系统等客观事物视为一个灰色的物质系统，在研究这些系统时，基于表征信息，利用灰色建模、灰色关联分析法等信息加工手段，探寻系统的内在规律，预见系统的发展状态，调控系统的发展速度，最后，实现系统物质和能量的优化组合。

灰色关联分析是灰色系统理论的一部分，建立在灰色空间概念的基础上，可以有效地处理灰色系统中不准确、不完整的信息。灰色关联是指系统中事物之间、要素之间，或者要素和行为间关系的不确定性。灰色关联分析方法发展迅速，已经被广泛地运用在系统分析、数据处理、建模和预测，以及控制和决策等方面。灰色关联评估系统通过计算各评价对象的灰色关联度来确定指标的等级，它只需要小样本数据，计算简单，然而预测精度却非常高，运用这种方法，可以克服传统相关分析方法不适合非线性模型的缺陷，尤其是在“贫信息”的条件下具有很好的效果.

(三)直觉决策理论

人的决策系统有两类，一是靠直觉决策，二是靠逻辑推理进行决策(也称为理性决策)。

直觉是人类认识过程中的有机因素，是思维能动性和创造性的一种表现，是由触发、联想、想象、顿悟所构成。直觉式应急决策不是按照逻辑逐步形成决策备选方案，制定行动路线，而是通过启发式对危机情境进行快速领悟后，自动激活大脑中已有的整套应急决策方案，一旦方案与危机情境相匹配，后续的应急决策加工过程便自动展开。

应急决策的隐性知识与直觉决策相联系。在运用直觉进行决策的过程中，决策者并没有经过缜密的逻辑推理，而是基于自身的知识、经验，直接获取解决问题的能力。与理性决策相比，直觉决策占用较少的认知资源，它是一种再认过程，是现实情景与先前经验知识的再认，是一种快速的识别模式。

直觉决策适用以下八种情况：1存在高度不确定性；2极少有先例存在；3变化难以科学地预测；4“事实”有限；5事实不足以明确指明前进道路；6分析性数据用途不大；7当需要从存在的几个可行方案中选择一个，而每一个的评价都良好；8时间有限，并且存在提出正确决策的压力。

直觉决策模型中，决策主体的经验模式处于核心地位，决策主体的知识、认知模式、决策效力、情感因素都受到经验的支配或影响，直觉决策机理如图1所示。

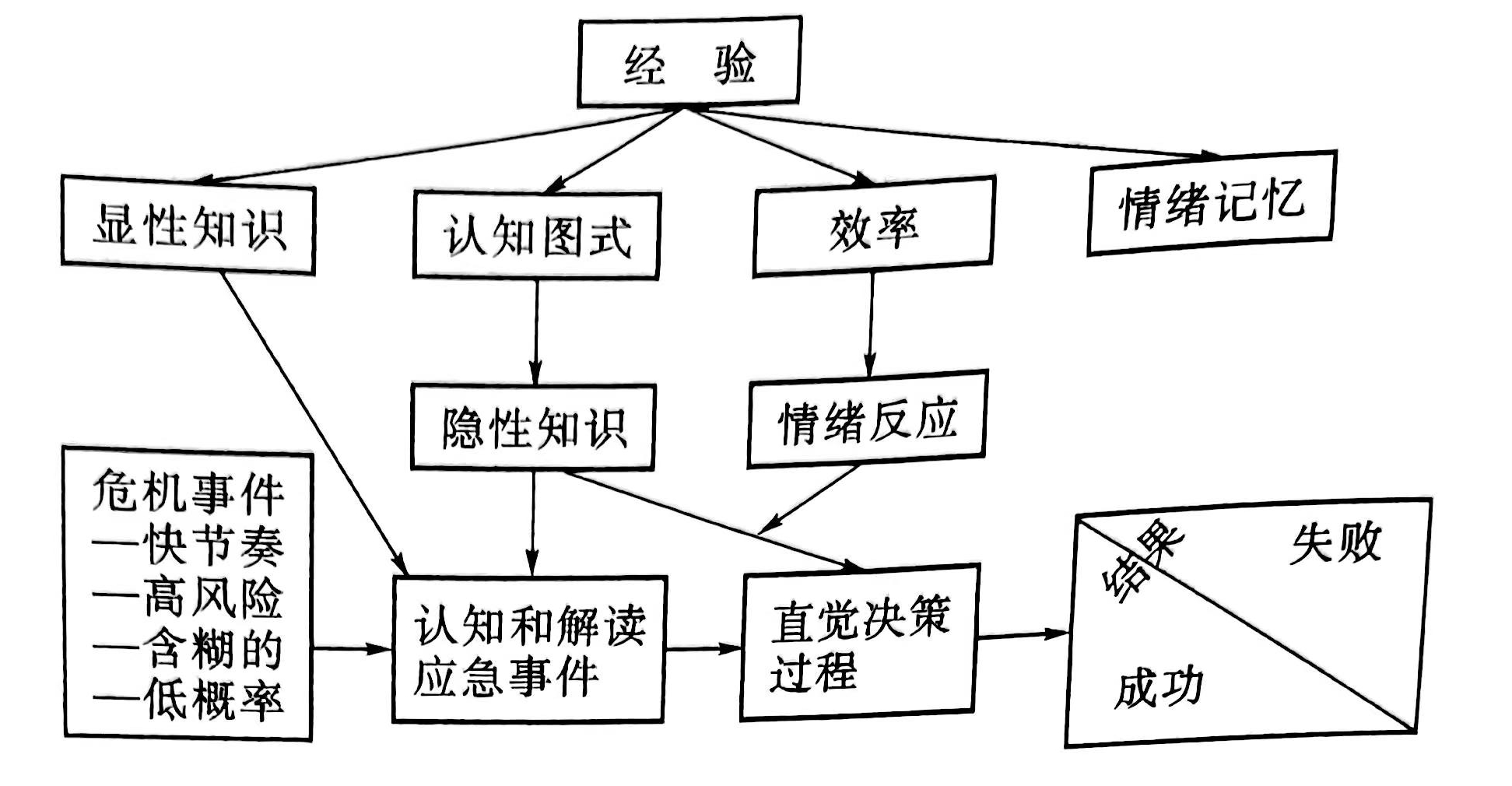
图1情绪在直觉决策中的角色

直觉决策不仅可以“再认”经验，还可以通过自身大量的相关知识、经验(并非直接相关经验)，激发顿悟、灵感，进行创新性决策，从而解决决策难题。

(四)多目标决策理论

多目标决策理论主要根据问题的多个属性对多个方案进行排序，从中选出最优方案。在决策过程中如果只考虑单个目标，称为单目标决策，如果需要考虑多个目标的满足程度，则是多目标决策问题。多目标决策是对两个或多个通常相互矛盾的目标进行科学评估，然后从备选方案中选取最佳方案的决策过程。要同时满足多个相互矛盾的目标是很难的，因此多目标决策实质上是在满足约束条件的前提下，寻求多个目标间的妥协，这一过程也称多目标最优化。单日标决策问题具有最优解，但多目标决策问题目标间可能存在矛盾性，通常无法找到最优解。在现实生活中，我们得到的通常是次优解，或称为非劣解。

(五)多属性效用理论

多属性效用理论(MAUT)是一种结构化、逻辑化、系统化的决策分析理论，主要用来评价在决策过程中起作用的各因素(属性)对决策结果的影响，并对其作出综合考虑，选出具有最高效用的方案。

MAUT方法解决问题的步骤如下：

（1）确定所有考虑的属性X=(x1，x2，......xn)；

（2）建立起各属性效用函数的表达式U(x)

（3）确立备选方案A=(A1，A2，......An)，

（4）计算各方案的效用Ui(X)，(i=1，2，…，m)；

（5）确定最佳方案。

·第i个方案的效用U（Ai)可按照下式计算。

U(Ai)=

式中：为第j个属性的权重，且≧0,；(dij)表示第i个方案第j个属性的效用值，计算出并且0≦(dij)≦1；j=1，2，...，n。

计算出所有方案的总效用后，对它们的总效用进行排序，效用最大的方案变为最优方案。